Rocket、MiniRocket、MultiRocket

# Rocket

# 摘要

大多数时间序列分类方法都具有很高的计算复杂度，即使对于较小的数据集也需要大量的训练时间，并且对于较大的数据集也难以处理。此外，许多现有的方法都专注于单一类型的特征，如形状或频率。基于卷积神经网络对时间序列分类的最近成功，我们证明了使用随机卷积核的简单线性分类器可以实现最先进的精度，而计算成本仅为现有方法的一小部分。使用这种方法，可以在不到2小时内在UCR档案中的所有85个“bake off”数据集上训练和测试分类器，并且可以在大约1小时内在超过100万个时间序列的大型数据集上训练分类器。

# 方法

主要思想：使用多个随机卷积核对时间序列进行转换，并使用转换后的特征来训练线性分类器

# 随机卷积核

为什么？

在UCR这种小数据集上使用卷积神经网络的效果并不是很好，因为卷积神经网络需要大量的数据进行训练，随机卷积核对这种小数据集可能会拥有更好的效果

Rocket与典型卷积神经网络中使用的卷积层，以及与之前使用卷积核（包括随机卷积核）的时间序列的工作有以下四个不同：

Rocket使用了大量的内核。由于只有一层核，并且不学习核的权重，计算卷积的成本很低，并且可以使用大量的核，而计算成本相对较低。
Rocket使用了大量不同的内核。与典型的卷积神经网络相反，在典型的卷积神经网络中，一组内核共享相同的大小、膨胀和填充，对于Rocket来说，每个内核都有随机的长度、膨胀和填充，以及随机的权重和偏差。
Rocket使用了内核膨胀。与卷积神经网络中膨胀的典型使用相反，在卷积神经网络中，扩张随着深度呈指数级增长，我们对每个内核随机采样膨胀，产生各种各样的内核膨胀，捕捉不同频率和尺度的模式，这对方法的性能至关重要。
除了对生成的特征使用最大池化，Rocket还使用了正值的比例(或ppv)。这使分类器能够在时间序列中衡量给定模式的流行程度。这是Rocket架构中最关键的一个元素，对其卓越的精度至关重要。

随机卷积核的特点：

长度：随机卷积核的长度以相同的概率从{7,9,11}中随机选择
权重：随机卷积核的每个权重从正态分布中采用，之后减去整体的均值，即，这样，使得大多数权重相对较小，当总体具有更大的幅度
偏置：偏置从均匀分布中采样，这样做的作用是，由于在计算ppv的时候，只有特征中的正值才会产生影响，这样对两个相似的卷积核，在拥有不同偏置的情况下，可以通过将特征中的值移到0以上或0以下，从而突出特征图中的不同方面
膨胀：膨胀从指数尺度进行采样，这里，保证了膨胀之后的卷积核的有效长度不超过输入时间序列的长度，膨胀使得其他相似的卷积核能以不同的频率和规模匹配相似的模式
填充（padding）：在生成卷积核时，将以相同概率随机决定是否对卷积核进行填充，若使用了填充，则在使用卷积核的时候，在每个时间序列的开始和结束处都会附加一个零填充量，以此使得时间序列中的每个点都能被卷积核的中间元素匹配（其实是排除膨胀的影响，因为膨胀之后卷积核的外围全是0，这样给时间序列加上合适的0填充就能使得时间序列的两侧被原本的卷积核所匹配），填充的长度为。在没有填充的情况下，卷积核就无法匹配时间序列的两端，而集中于时间序列中心区域的模式。

其他细节： 在进行卷积计算时，步长永远为1，同时不使用非线性激活函数，并且输入的时间序列经过归一化，即处理为均值为0，方差为1的形式，卷积核的个数为超参数，默认值为10000

# 时间序列变换

每个卷积核应用于每个输入时间序列，产生一个特征映射，卷积运算涉及卷积核和输入时间序列之间的滑动点击，从中的位置开始，对给定时间序列应用具有膨胀和偏差的核 $ω$ 的结果如下：

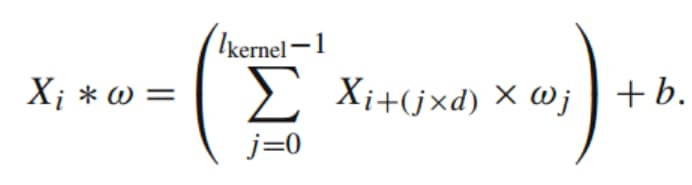
Rocket从每个特征映射中计算两个聚合特征，即对于每个时间序列，每个卷积核会生成两个实数作为特征，分别是最大值（最大池化）以及ppv（，其中，是卷积运算的输出）

也就是说，对于k个内核，Rocket会在每个时间序列中生成2k个特征；对于10000个内核，Rocket会生成20000个特征，对于较小的数据集（例如UCR档案上的所有数据集），特征的数量可能比数据集中的实例数量或每个时间序列中的元素数量大得多。

# 分类器

将转换后的特征用于训练线性分类器，当数据集的长度小于特征的数量（即默认情况下，少于20000个训练样本）时，使用岭回归分类器（ridge regression classifier），否则使用一般的逻辑回归。

逻辑回归Rocket可以与逻辑回归和随机梯度下降一起使用。这特别适合于非常大的数据集，因为它提供了固定内存成本的快速训练(由每个小批的大小固定)。转换可以在每个小批上执行，也可以在数据集的较大部分上执行，然后将其进一步划分为小批进行训练。

然而，对于UCR档案中的所有数据集，我们使用岭回归分类器，其中岭回归模型以“one versus rest”的方式为每个类训练，并具有L2正则化。

当特征的数量显著大于训练示例的数量时，正则化是至关重要的，它允许线性模型的优化，并防止迭代优化中的病态行为，例如，对于逻辑回归。岭回归分类器可以利用泛化交叉验证快速确定适当的正则化参数。我们发现，对于较小的数据集，岭回归分类器在实践中明显快于逻辑回归，同时仍能实现较高的分类精度。我们发现，对于较小的数据集，优化逻辑回归的多个超参数(小批量大小、学习率、正则化等)以达到与岭回归分类器相同的分类精度明显更具挑战性和耗时。

# 限制

Rocket的一个限制是，为了达到最高的分类精度，需要大量的卷积核，这反过来又限制了分类器的选择，即那些对大量特征有效的分类器(包括岭回归分类器和逻辑回归)。另一个限制是，在使用固定的随机卷积核时，对于非常大的数据集，学习可能会在某个时候“饱和”。我们期望更多典型的卷积神经网络架构与学习内核，如InceptionTime，在非常大的数据集上实现更高的精度，尽管计算成本要高得多。然而，Rocket至少可以用于非常大的数据集，而许多现有的时间序列分类方法都不能，并且我们注意到，卫星图像时间序列数据集的准确性似乎只在大约50万个训练示例之后才趋于稳定(参见第4.2节)。Rocket目前只配置为使用单变量时间序列。Rocket的扩展到多元时间序列和应用到非常大的数据集是未来工作的重点。

# MiniRocket

# 摘要

Rocket通过使用随机卷积核转换输入时间序列，并使用转换后的特征来训练线性分类器，从而实现了最先进的时间序列分类精度，而计算成本仅为大多数现有方法的一小部分。我们重新设计了一种新的方法，迷你火箭。在更大的数据集上，MiniRocket的速度比Rocket快75倍，而且几乎是确定的(可选的是完全确定的)，同时保持本质上相同的精度。使用这种方法，可以在10分钟内在UCR档案的所有109个数据集上训练和测试分类器，达到最先进的精度。 MiniRocket比任何其他具有相当精度的方法(包括Rocket)都要快得多，并且比任何其他计算成本类似的方法都要准确得多。

# 方法

主要思想：在Rocket的基础上，移除几乎所有的随机性，提高算法的运行速度

# 移除随机性

Rocket使用从{7,9,11}中随机选择长度的内核，从N(0,1)中抽取权重，从U(-1,1)中抽取偏置项，同时拥有随机膨胀和随机填充。两个特性，PPV和max，是根据每个内核计算的，总共有20,000个特性。MiniRocket的特点是内核在长度、权重、偏置、膨胀和填充方面进行了许多关键更改，以及对特性的相应更改，如下表所示。

变化如下：

长度：MiniRocket使用长度固定为9的卷积核，由于MiniRocket的权重修改为2个固定取值，所以可能的卷积核数量会随着卷积核的长度呈指数级增长，因此在进行权衡之后， MiniRocket最后将卷积核的长度设定为9，这样就有个可能的卷积核，但这些卷积核并非全部使用，而是从中再挑选84个卷积核，这84个卷积核组成的子集平衡了精度和使用少量内核的计算优势。
权重：权重被设定为2个值，即和，且在卷积核内，保证存在6个和3个，原文解释说，由于计算PPV时权重的大小并不重要，因为PPV的计算公式决定了其本身的分布并不重要，因为偏差值是从卷积的输出中计算得到的，这样将卷积核的所有权重设为均值为0的情况就不需要对输入进行标准化了，此外，设置卷积核的个数为84并不是就设定特征数量只从这84个卷积核中得出，将和的值取反，也有同样的效果，但并不需要对其进行额外的计算。尽管这样，这套设定的内核其实并没有特别的地方，其他长度为9的内核也能产生相应的精度，包括Rocket中随机的权重，这样做只是移除了随机性，减少了计算量。
偏置：MiniRocket的偏置从卷积输出中提取，并用于计算PPV。具体做法为随机选择一个时间序列，计算卷积输出，将[0.25,0.5,0.75]作为阈值，在那几个位置的卷积输出作为整体计算PPV的偏置
膨胀：MiniRocket中膨胀的范围为，这里指数项的范围为到，其中是输入序列长度，是卷积核长度。MiniRocket设置默认最大膨胀值为32。
填充（padding）：与Rocket中随机填充不一样，MiniRocket对每个卷积核/膨胀组合交替使用填充，令一半卷积核/膨胀组合使用填充，另一半不使用，且使用标准的零填充，即在时间序列的开始和结束都加0。
特征：与Rocket相比，MiniRocket放弃了计算max，保留了PPV，每个时间序列最后产生的特征数量约为10000个（实际是9996个，卷积核数量84的倍数，因为卷积核的膨胀，时间序列填充都会影响最后的结果，生成新的特征）

# 优化后的时间序列转换

MiniRocket在速度上与Rocket相比具有显著提高，这得益于以下的优化

同时计算和的PPV：由于所选择的84个卷积核可以取反得到另外一组84个卷积核，这些卷积核在后续训练的结果都可以从之前那84个卷积核的计算结果中得到，例如卷积输出的特征其实都是变换了一下符号，偏置也是相反的，因此在计算PPV时，不需要重复计算，只需要计算PNV即可，其中有，而计算出来的PNN就是的PNV，因此只需要一次计算。
重复利用卷积核的输出去计算多个特征：对于给定的卷积核和膨胀系数，但具有不同的bias，可以重复利用卷积输出计算得到多组特征
避免了卷积运算中的乘法：由于卷积核中的权重为-1和2，因此可以使用卷积计算中的一些小技巧去避免乘法计算
对于每次膨胀，几乎在一次计算所有的卷积核？？？

# MultiRocket

# 摘要

我们提出了MultiRocket，这是一种快速时间序列分类(TSC)算法，它可以在很少的时间内达到最先进的精度，并且没有许多最先进方法的复杂集成结构。 MultiRocket在MiniRocket(迄今为止最快的TSC算法之一)的基础上进行了改进，通过添加多个池化操作符和转换来提高生成特征的多样性。除了处理原始输入序列外，MultiRocket还应用一阶差分对原始序列进行变换。卷积应用于两个表示，四个池运算符应用于卷积输出。当使用加州大学河滨分校TSC基准数据集进行基准测试时，MultiRocket明显比MiniRocket更准确，并且在精度方面与目前排名最好的方法HIVE-COTE 2.0竞争，同时速度要快几个数量级。

# 创新

# 一阶差分

为什么要使用一阶差分？

时间序列的一阶差描述了时间序列在每个单位步上的变化，这对于原始的时间序列来说，是一个额外的信息，例如识别时间序列的斜率或时间序列中某些异常值(或模式)的存在，这些异常值可能更容易区分两个类别。

具体做法

# 卷积核

MultiRocket中卷积核的长度、权重、膨胀、偏置、填充与MiniRocket一致

# 四种池化

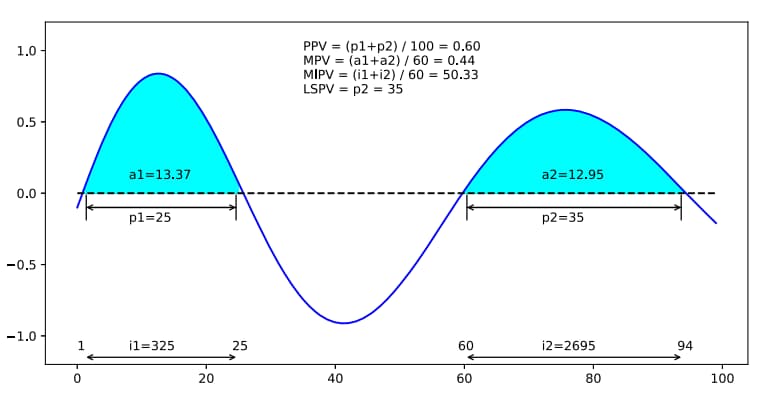
Proportion of Positive Values (PPV)：

PPV能够捕获反映输入和给定模式之间的弱匹配的时间序列的比例。和rocket一样，只需要计算Z中大于0的值，大于0的值记为Postive value，看postive value的个数与序列长度的占比，公式如下，其中n为序列的长度。

Mean of Positive Values (MPV)：

MPV捕捉输入时间序列和给定模式之间的匹配强度——计算PPV时可用但被丢弃的信息。所有positive的值相加，求postive的均值。其中m为postive values的个数。

Mean of Indices of Positive Values (MIPV)：

MIPV捕获关于卷积输出中positive values的相对位置的信息。每个postive value的位置（索引）的均值。如果一个output Z没有Postive values，那就将MIPV设置为-1。公式如下：

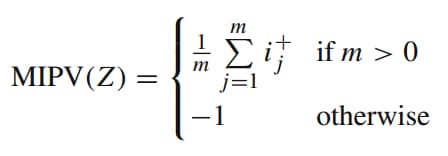
Longest Stretch(拉伸) of Positive Values (LSPV)：

MIPV汇集所有正值，因此无法区分连续正值的许多小序列和少量长序列。第一次出现postive values的索引位置与最后一次出现postive values的索引位置之差。

计算示例：

编辑

上次更新: 2024/05/30, 07:49:34

← SwingTransformer A survey on semi-supervised learning→